El problema de los puentes de Königsberg
Durante una época dediqué mis esfuerzos a propiciar lo que ahora se llama Computational Think a través de la programación lógica. Había una forma de analizar los problemas, era a través de la búsqueda en profundidad en esquemas arborescentes, habiendo transformado previamente los problemas en esquemas en árbol, es decir habiendo obtenido una representación de este tipo del problema.
Se trataba de implementar esquemas lógicos a través del lenguaje de programación Prolog. Simplificando mucho es lo que hacía con la geometría, la recursividad o la modularización LOGO. Todo ello concluyó en la edición de un libro, del que ahora queda algún ejemplar por las librerias de viejo:
TÉCNICAS DE PROGRAMACIÓN DECLARATIVA EN EL AULA. TURBO PROLOG 2.00.
ZAPATA ROS, Miguel.
De él sacamos lo que sigue.
El problema de los puentes de Könisberg y el backtraking
En la programación declarativa, en determinadas ocasiones interesa
cortar la búsqueda en profundidad y provocar el Backtracking en un punto
determinado.
Esto sucede cuando, por ejemplo, queremos obtener una única
respuesta a una interrogación, y previsiblemente el programa contiene alguna
bifurcación.
También sucede cuando el programa tiene un crecimiento desmedido
en función de la abundancia de nodos del árbol correspondiente, o de cláusulas
dobladas o triplicadas.
En este caso se produce lo que se llama una “explosión
combinatoria" o un “crecimiento exponencial”. De tal manera que el
ordenador puede perderse en la búsqueda o verse desbordado en su capacidad por
un crecimiento de este tipo.
Otra ocasión en que, por ejemplo, conviene cortar la búsqueda se
produce cuando el ordenador cae en un bucle sin fin.
Otras veces lo que interesa es provocar la vuelta atrás aunque
ésta no tenga en buena lógica por qué producirse. De tal manera que una vez
conseguido un objetivo parcial y satisfecha una cláusula, el ordenador se
comportase a todos los efectos como si la búsqueda hubiera fallado, forzando
con ello seguir la búsqueda en profundidad en esa rama por si hubiera más
cláusulas que la satisfaciesen, en vez de esperar a que se culminase la vuelta
atrás.
Este recurso interesa sobre todo cuando queremos que se produzcan
una serie de acciones en un determinado orden. Es decir que funcione, el
programa y el sistema, de modo procedimental.
Para ambos fines -corte y fallo- existen en Turbo Prolog dos
predicados predefinidos: ! (CORTE) y
FAIL (FALLO).
Veamos ahora con más detenimiento cómo funcionan. Para ello vamos
a utilizar varios ejemplos. Uno de ellos nos lo proporciona el problema de “Los
puentes de Kónigsberg”:
Königsberg (hoy Kaliningrado) es una ciudad de la Prusia oriental
(donde nació, murió y vivió toda su vida Immanuel Kant), en la parte que
actualmente pertenece a la Federación Rusa, cruzada por el río Pregel (hoy
Pregolya) que forma dos islas, entre las cuales y las dos orillas habí una
serie de siete puentes:
Mapa de Königsberg en la época de Leonhard Euler, que muestra dónde
se encontraban los siete puentes (en verde claro) y las ramas del río (en
celeste).
http://upload.wikimedia.org/wikipedia/commons/thumb/5/5d/Konigsberg_bridges.png/300px-Konigsberg_bridges.png (URL de la imagen)
En la actualidad en Google Maps
lo podemos ver:
Dos
de los siete puentes originales no sobrevivieron al bombardeo de Königsberg en
la Segunda Guerra Mundial. Otros dos puentes fueron posteriormente demolidos y reemplazadas
por una moderna autopista. Los otros tres puentes se mantienen, aunque sólo dos
de ellos son de la época de Euler (uno fue reconstruido en 1935).
Por
lo tanto, a partir de 2000 , en la actualidad hay cinco puentes en
Kaliningrado.
En rojo los que se
conservan, al menos en su posición. En azul los que no existen.
Vista
de STREET VIEW desde el puente que une
las dos islas,
que las unen según el esquema.
En la época en que escribimos el libro no existía Google Maps.
Utilizamos algo más esquemático:
Las gentes de esta ciudad discutían frecuentemente sobre si era
posible ir de una orilla a la otra pasando por todos los puentes una sola vez.
Este problema alcanzó fama en su tiempo y fué finalmente resuelto
en sentido negativo por Euler en 1.736.
No obstante es frecuentemente utilizado, aún hoy día, como ejemplo
en Topología, Teoría de Grafos, etc.
En el libro lo utilizamos como hemos visto como ejemplo para
ilustrar Backtraking, corte y fallo. Lo
formalizamos utilizando para ello un programa Prolog. Lo hacemos en pasos
sucesivos y aprovecharemos para comentar los predicados “corte” y “fallo”.
A los amigos prologueros
proponemos completar el programa para resolver el problema
completo utilizando PROLOG
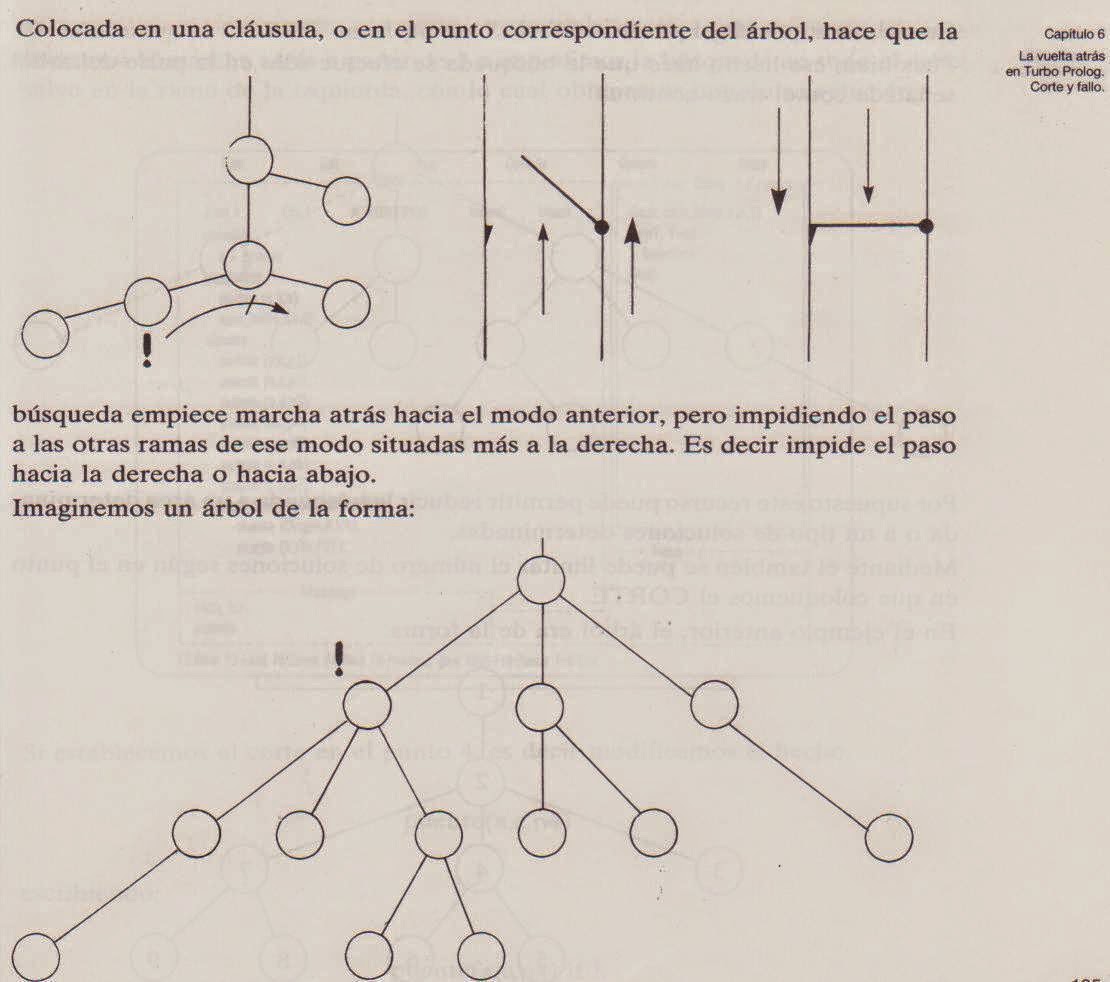
El procedimiento en esencia viene ilustrado en las cuatro páginas
que adjuntamos:











Siempre he querido estudiar algo más, pero con el trabajo se me hace imposible. Me han dicho que estudiar en este sitio https://1cursos.com/te-cursos-de-acceso-a-fp distancia podría ser una opción, pero no sé si realmente funcione para mí.
ResponderEliminar